今回は令和2年(2020年)の第2問 設問2を取り上げ、意思決定会計(NPV、デシジョンツリー)の問題について、どのような思考プロセスで解答に至るのかを具体的に解説します。(あくまでも、「私ならこのように解答する」という参考例として記載していますので、その旨ご承知おきください。)
なお、この第2問は設問1がCVP分析で、設問2は意思決定会計というハイブリッド構成となっています。設問1の内容はこちらで解説しています。
問題の確認
令和2年(2020年)の問題はこちらに掲載されています。
問題文の確認
まずは、問題文から確認しましょう。
以下は、設問文のポイントを落とさないように記載するマークの例です。



解答案
この設問2・3は、「効果がある場合」や「ない場合」などという条件をもとにその効果を確率的に求め、最終的にどのシナリオを採用すべきかという意思決定を行う「デシジョンツリー」という問題に分類されます。それぞれのシナリオの価値と発生確率を考慮して、最も合理的な選択肢を見つけるための分析手法であり、木の枝が分かれていくような図で表現するため、このように呼ばれます。
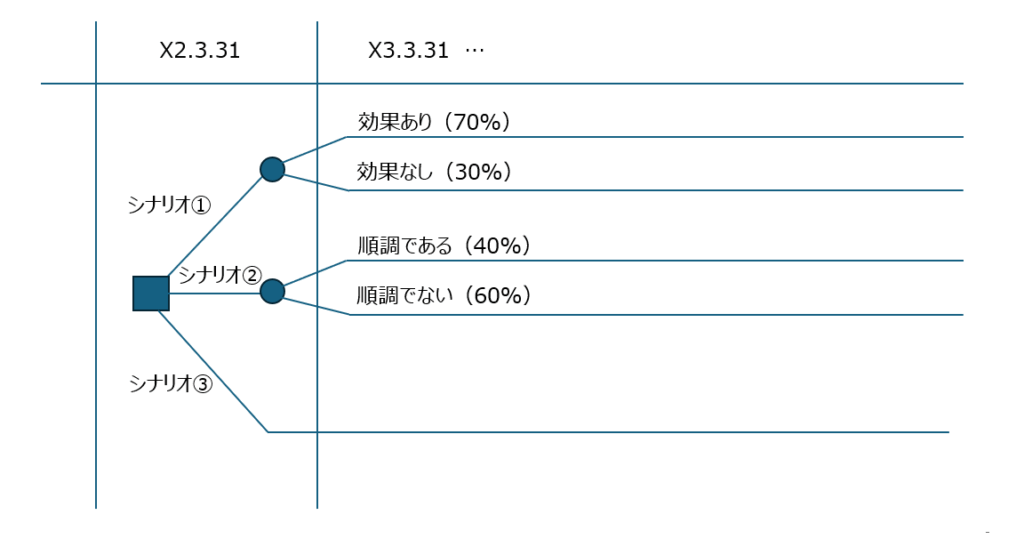
(a) シナリオ①:広告宣伝を継続する場合
問題の概要
選択肢②は、毎年広告費を支払うシナリオです。「効果がある」場合と「効果がない」場合の営業CFから、投資効果の期待値を求めます。
広告費は期首の4/1に支払い、その効果を図るのは期末の3/31となっているためNPVの計算の際には考慮が必要です。また、効果がない場合は3年で打ち切られる点にも注意しましょう。
具体的な計算
(1) 投資効果ありの場合
| X2.4.1 | X3.3.31 | X4.3.31 | X5.3.31 | X6.3.31 | X7.3.31 | |
|---|---|---|---|---|---|---|
| 広告費 | -5 | -5 | -5 | -5 | -5 | |
| 営業CF | 35 | 35 | 35 | 35 | 35 | |
| 処分価額 | 24 |
広告費は期首に支払っているので、例えば支払日はX3.4.1などとなりますが、便宜上X3.3.31(前期末)の支出として計算します。
X2年末(X2.3.31=X2.4.1)時点の現在価値は現価係数を用いて、以下の様に計算できます。
効果ありNPV = -5×(1+0.926+0.857+0.794+0.735) + 35×(0.926+0.857+0.794+0.735+0.681) + 24×0.681 = 134.539百万円
(2) 投資効果なしの場合
| X2.4.1 | X3.3.31 | X4.3.31 | X5.3.31 | X6.3.31 | X7.3.31 | |
|---|---|---|---|---|---|---|
| 広告費 | -5 | -5 | -5 | |||
| 営業CF | -5 | -5 | -5 | |||
| 処分価額 | 28 |
効果なしの場合は、3年目で広告費を打ち切り、資産も処分されるため、キャッシュフローは上記のようになります。
X2年末(X2.3.31=X2.4.1)時点の現在価値は現価係数を用いて、以下の様に計算できます。
効果なしNPV = -5×(1+0.926+0.857) + (-5)×(0.926+0.857+0.794) + 28×0.794 = -4.568百万円
(3) 期待値
(1)の効果ありとなる確率は70%、(2)の効果なしとなる確率は30%なので、以下の様に期待値を計算する。
NPV = (1)のNPV(134.539)× 0.7 + (2)のNPV(-4.568)× 0.3 = 92.8069 ≒ 92.81(百万円)
解答
※このような問題は、条件が多く計算にも時間がかかるため、後回しもしくは捨て問扱いにする方が多いと思います。ただし、どのような解答方針で解くかということだけでも(ⅰ)に記載しておきたいところです。(例えば以下の(ⅰ)の解答案で太字にした部分)
(ⅰ)
投資効果あり、なしの場合に分けて正味現在価値(NPV)を求め、それぞれの確率をかけて期待値を求める。
(1) 投資効果ありのNPV = -5×(1+0.926+0.857+0.794+0.735) + 35×(0.926+0.857+0.794+0.735+0.681) + 24×0.681 = 134.539百万円
(2) 投資効果なしのNPV = -5×(1+0.926+0.857) + (-5)×(0.926+0.857+0.794) + 28×0.794 = -4.568百万円
NPV=(1)×0.7 + (2)×0.3 = 92.8069 ≒92.81(百万円)
(ⅱ) 92.81 (百万円)
(b) シナリオ②:業態転換する場合
問題の概要
選択肢②は、改装工事による業態転換のシナリオです。ここでも「順調な場合」と「順調でない場合」に分岐するため、NPVの期待値を計算します。
分析にあたり、以下の点に注意しましょう。
- 初年度のCF: 初年度の営業CFは、通常の半額として計算します。
- 減価償却費: 減価償却費の扱いが論点となり得ますが、本問で与えられているのは税引後の「営業CF」であるため、減価償却費に伴うタックス・シールドなどは既に考慮済みと判断します。
具体的な計算
(1) 順調な場合
| X2.4.1 | X3.3.31 | X4.3.31 | X5.3.31 | X6.3.31 | X7.3.31 | |
|---|---|---|---|---|---|---|
| 投資額 | -30 | |||||
| 営業CF | 12.5 | 25 | 25 | 25 | 25 | |
| 処分価額 | 27 |
投資はX2年期首に行っています。また、設問の条件より、X3.3.31では25百万円の1/2のCFです。減価償却費については、営業CFに含まれており、この問題では考慮しません。
X2年末(X2.3.31=X2.4.1)時点の現在価値は原価係数を用いて、以下の様に計算できます。
順調な場合のNPV = -30 + 12.5×0.926 + 25×(0.857+0.794+0.735+0.681) + 27×0.681 = 76.637百万円
(2) 順調でない場合
| X2.4.1 | X3.3.31 | X4.3.31 | X5.3.31 | X6.3.31 | X7.3.31 | |
|---|---|---|---|---|---|---|
| 投資額 | -30 | |||||
| 営業CF | 7.5 | 15 | 15 | 15 | 15 | |
| 処分価額 | 27 |
(1)の場合と違うのは営業CFのみです。
X2年末(X2.3.31=X2.4.1)時点の現在価値は原価係数を用いて、以下の様に計算できます。
順調でない場合のNPV = -30 + 7.5×0.926 + 15×(0.857+0.794+0.735+0.681) + 27×0.681 = 41.337百万円
(3) 期待値
(1)の順調な場合の確率は40%、(2)の順調ではない確率は60%なので、以下の様に期待値を計算する。
NPV = (1)のNPV(76.637)× 0.4 + (2)のNPV(41.337)× 0.6 = 55.457 ≒ 55.46(百万円)
解答
(ⅰ)
営業が順調な場合、順調ではない場合に分けて正味現在価値(NPV)を求め、それぞれの確率をかけて期待値を求める。
(1) 順調な場合のNPV = -30 + 12.5×0.926 + 25×(0.857+0.794+0.735+0.681) + 27×0.681 = 76.637百万円
(2) 順調でない場合のNPV = -30 + 7.5×0.926 + 15×(0.857+0.794+0.735+0.681) + 27×0.681 = 41.337百万円
NPV=(1)×0.4 + (2)×0.6 = 55.457 ≒ 55.46(百万円)
(ⅱ) 55.46 (百万円)
(c) 最適な意思決定
問題の概要
①、②、③のどのシナリオが最適なのかを問う問題です。
基本的な考え方
- ①:92.81(百万円)
- ②:55.46 (百万円)
- ③:30(百万円)※処分価額がCFになると考える
以上よりシナリオ①の投資効果が最も高い。
解答
※(a)(b)でそれぞれのシナリオにおけるNPVが求められなかった場合でも、この解答欄には①~③の何かを書きましょう。(書かなければゼロ点が確定します)
なお、このような問題の場合、①②を計算させたにもかかわらず結局処分するだけの③を採用する確率は低いものと考えますのでまず除外します。また、①と②を比較した場合、①は「効果あり」の場合が70%であるのに対して、②は「順調な」場合が40%となっており、ポジティブな確率が高い①が採用される可能性が高いと推測できます。
①
以上となります。



コメント